Lambda calculus is one of the two most well known models of computation.
The basic element of the lambda calculus is the lambda. Essentially, it's a function of one variable. Let's just jump into some examples, because that's easier than explaining it with words.
Here's the identity function:
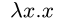
We can apply this to another variable or lambda. For example,
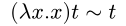
We can make lambdas that take two inputs by nesting lambdas. This function returns its first input:
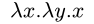
For example,
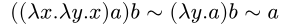
We can clean up this notation somewhat:
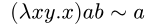
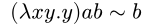
Essentially, lambdas take some variable, and replace all instances of that variable in the body with the input.
is a specific way of writing lambda calculus expressions.
I chose this particular notation because parsing expressions with variable names, parentheses, and scope is kind of annoying. Binary lambda calculus side-steps all of that.
There are three types of symbol in BLC.
Lambdas are notated with a 00. They are followed by one term which serves as the function body.
Application is notated with a 01. This is equivalent to starting a pair of parentheses which contains only the next two terms.
Variables are a series of 1's followed by a 0. The number of 1's tells you which lambda's input it's referring to. 10 is the input of the lambda it appears in. 110 is the input of the lambda above that, and so on. This indexing is called the De Bruijn index.
I go through these symbols and create a tree-like structure, which can be reduced according to the usual rules of lambda calculus.
Now that the "binary" part is out of the way, I can basically just yap about how I simplify lambda expressions in my program, and about lambda calculus in general :D
I chose to use normal order reduction, wherein the first, outermost, reducible application is the one that gets reduced first. This isn't the most efficient reduction strategy, but it always results in what's called the "normal form" of the expression (if it exists), which is usually the expected output.
The De Bruijn indexes do complicate this slightly. When you reduce a lambda, the indexes that don't get replaced, and which refer to a lambda outside of the one getting reduced, all need to be decreased. This is still easier than dealing with actual variable names, though.