


Cantellated 24-cell
Runcinated 120 cell (very close to the camera)
5D demicube
Very roughly, Wythoffian polytopes are the platonic solids, and most Archimedean solids, in all dimensions.
More accurately, a Wythoffian polytope is a shape that can be represented by a Coxeter-Dynkin diagram. There's a lot to be said about this, but to get a general idea of what this means, let's look at an example.
This is the Coxeter-Dynkin diagram of a cube. Each node represents a mirror, and the edges tell us about the angles between these mirrors. No edge means the mirrors are orthogonal, an unlabeled edge represents an angle of π/3, and an edge labeled with some number n represents an angle of π/n
From the diagram shown, then, we know there are 3 mirrors. Two of them are orthogonal. The third has angles of π/3 and π/4 with the other two.
These mirrors define a set of regions called "Weyl chambers," such that reflections across mirrors map Weyl chambers to other Weyl chambers. Since our final shape is basically a tiling of a hypersphere, we are most interested in where these Weyl chambers intersect with that hypersphere. These are called fundamental simplices, and correspond to the polytope's flags.
You might notice the leftmost node is ringed. This specifies that each vertex is some distance away from the mirror represented by that node. This tells us where the vertex is within each fundamental simplex / flag.
We can use this to find all the vertices, and use relationships between the flags to find all the edges, faces, and other elements.
The first problem I faced when trying to generate Wythoff constructions was finding a valid set of mirrors from a Coxeter-Dynkin diagram. If I could find one set of mirrors, I could use it to generate all of the flags.
I came up with what I think was a pretty clever solution.
Consider a matrix L, whose columns are the normal vectors of the mirrors we want.
We know what the angle should be between each pair of vectors, using the Coxeter-Dynkin diagram.
If we utilize the fact that matrix multiplication gives you the dot products of all the rows of one matrix with the columns of another, we know that the following must be true:
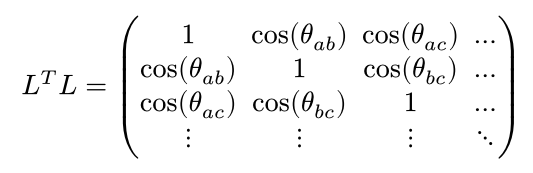
Luckily, this is a solved problem! It's called the Cholesky decomposition. The Cholesky decomposition of the above matrix will give us the matrix L whose columns are the mirrors' normal vectors.
We can think of compositions of reflections - corresponding to different fundamental simplices - as nodes on a graph. Each graph edge, then, shows which simplices are related by a single reflection.
To generate this graph, we start with the node which represents no reflections. We generate the remaining nodes by repeatedly composing reflections, almost like traversing a tree, until we visit a flag we've already been to. Then we know these nodes are the same and they can be connected accordingly.
As of writing this, my program only finds the edges, and it does it in a really bad slow way. I want to upgrade it to find all the relationships between groups of fundamental simplices, so that it can easily generate all the polytope's elements, but it's not there yet.
For now, it works as follows:
First, it finds the vertices. This is pretty easy because we have the vertices of each fundamental simplex, and this corresponds nicely to how ringing nodes moves the vertex within the fundamental simplex. Each vertex is just some combination of each fundamental simplex's vertices.
Then, it much less elegantly finds the edges. It does an O(n log(n)) search of all the fundamental simplices, searching for pairs which share all but one vertex. It connects the polytope vertices associated with these fundamental simplices with edges. It doesn't generate other elements -w-
I hope to improve this in the future, but for now, it works, and the wireframe renders look nice :3



Cantellated 24-cell
Runcinated 120 cell (very close to the camera)
5D demicube
This version of the renderer is entirely the work of Tessimal. I wrote a rudimentary wireframe renderer before this, but with theirs, you can actually see what's happening.